Backpropagation

Intro

Präsentation ist auch online sirbubbls.github.io/backpropagation-seminar

GitHub: https://github.com/sirbubbls/backpropagation-seminar

Zusätzliche Ressourcen

Deep Learning (Ian Goodfellow, Yoshua Bengio & Aaron Courville)

https://www.deeplearningbook.org

Backpropagation Kapitel

Jupyter Notebook

Beispiele für alle praktischen Beispiele dieser Präsentation sind in diesem Repository zu finden.

Agenda

1. Vorwissen
   • Gradients & Stochastic Gradient Descent
   • Computational Graphs
2. Neuronale Netze
3. Forward Propagation
4. Backpropagation
   • Kettenregel
   • Backpropagation
   • Implementation in Python
5. General Backpropagation
6. Historisches
7. Quellen

Vorwissen

Gradient

Der Gradient ist der Vektor aller partiellen Ableitungen einer Funktion \(f\).

Notation: \(\nabla f(x)\)

Beispiel

\(f(x) = 2x_1^2 + x_2^3\)

\(\rightarrow \nabla_xf(x)=\left(\begin{array}{c} f'_{x_1} \\ f'_{x_2} \end{array}\right)= \left(\begin{array}{c} 4x_1 \\ 3x^2_2 \end{array}\right)\)

Jacobi Matrix

Bei mehreren Funktionen (o.a. Komponenten Funktionen).

Bei mehreren Funktionen bilden deren Gradienten eine Jacobi Matrix.

\[ J(f) =\left (\begin{array}{cc} \nabla f_1 \\ \nabla f_2 \end{array} \right ) \]

Stochastic Gradient Descent

Der Gradient Descent Algorithmus wird dafür verwendet ein lokales Minimum einer Funktion zu bestimmen.

Beispiel

Funktion \(f(x)=x_1^2-x_2^2\) ist gegeben.
Also: \(\nabla_xf(x)=\left(\begin{array}{c} f'_{x_1} \\ f'_{x_2} \end{array}\right)= \left(\begin{array}{c} 2x_1 \\ -2x_2 \end{array}\right)\)
Wir starten mit einem beliebigen Punkt: z.B. \(\left(\begin{array}{c} 2 \\ 1 \end{array}\right)\) und setzen ein:
\(\left(\begin{array}{c} 2x_1 \\ -2x_2 \end{array}\right) = \left(\begin{array}{c} 2 * 2 \\ -2 * 1 \end{array}\right) = \left(\begin{array}{c} 4 \\ -2 \end{array}\right)\)

\(Neuer\ Punkt = \left(\begin{array}{c} 2 \\ 1 \end{array}\right) - \lambda \left(\begin{array}{c} 4 \\ -2 \end{array}\right)\) mit \(\lambda: learning\ rate\)

Visualisiert

Computational Graphs

Typischerweise werden Operationen in artificial neural networks nicht mit mathematischen Formeln angegeben, sondern als Graph dargestellt.

Repräsentation

Jede Node in einem Graph \(G\) repräsentiert eine mathematische Operation oder eine Input Variable.

Beispielsweise:

• Matrix Multiplikation
• Addition
• Skalare Multiplikation

Addition Beispiel

\[ y = a+b \]

Komplexere Beispiele

\(x=y+z\)
\(a=x\odot z\)

Künstliche Neuronale Netze & Deep Learning

Künstliche Neuronale Netze

Als Vorbild dienen Neuronale Netze in der Biologie, jedoch sind beide Felder doch unterschiedlicher als man vielleicht erwarten würde.

In diesem Vortrag werden nur fully connected feed forward networks behandelt.

Formale Definition

Parameter werden üblicherweise als Theta (\(\theta\)) notiert.
Der Lernalgorithmus soll die Parameter \(\theta\) so verändern, dass sich \(f\) so nah wie möglich an \(f^*\) annähert.

Formale Definition für ein neuronales Netz: \(y=f(x; \theta)\) und \(y = f^*(x)\)

• \(y\) ist den Wert den unser NN voraussagen soll
• \(x\) sind die Input Daten, die das NN erhält
• \(\theta\) sind alle Parameter eines neuronalen Netzwerks
• \(f^*\) ist unsere Zielfunktion

Wie ist nun ein neuronales Netzwerk aufgebaut?

Wir teilen das Netzwerk in Schichten (Layer) auf.

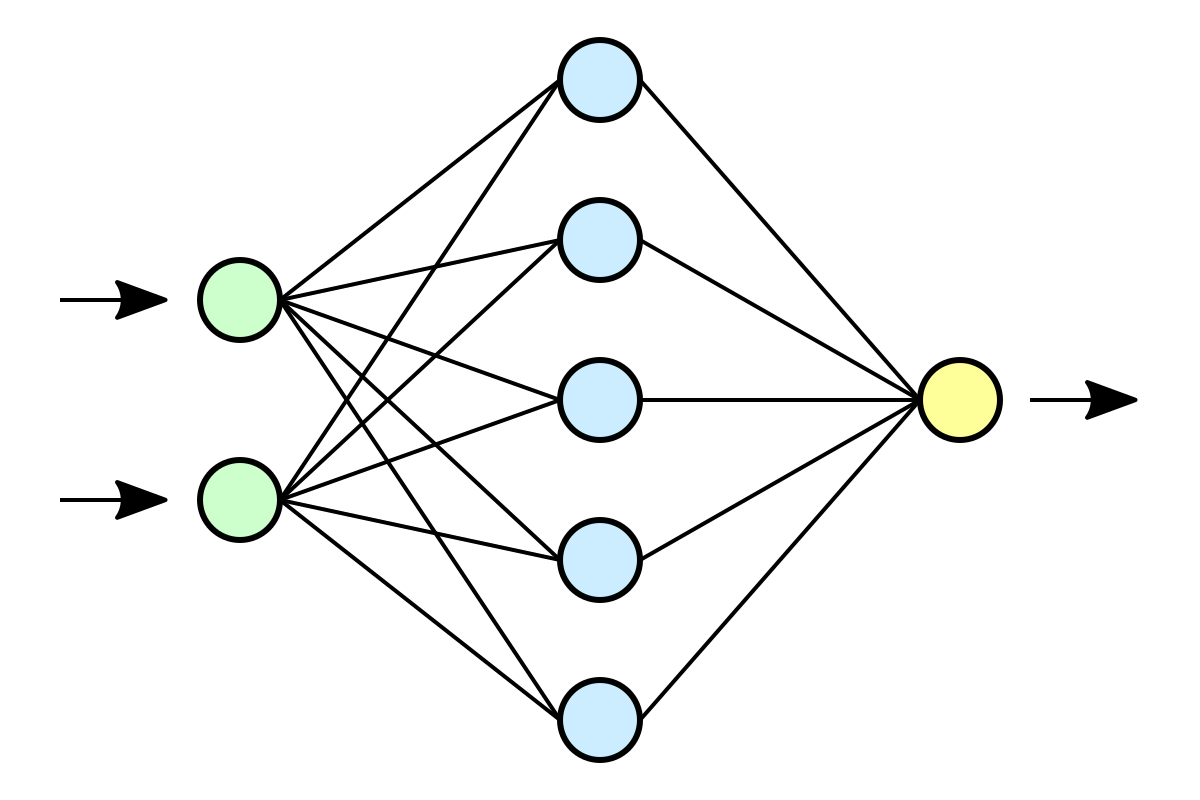
Jeder Layer bildet eine Funktion \(f^{i}\), mit \(i=Layer\ Index\) ab.

Formell

Somit ist ein neurales Netzwerk eine Kette an Funktionen \(f\).

Ein Netz mit \(3\) Layern wäre somit \(f^2(f^1(f^0(X)))\) mit \(X=Input\ Data\)

Aufbau eines Layers

Jeder Layer enthält mindestens folgende Informationen:

• Eine Weight Matrix (\(w\))
• Einen Bias Vektor (\(b\))
• Aktivierungsfunktion (\(\sigma\))

Verbindung der Layer

Jedes Neuron eines Layers \(L_i\) ist mit allen Neuronen des Layers \(L_{i-1}\) verbunden.

Aktivierungsfunktion

Da wir bei Neural Networks oft versuchen non-lineare Zusammenhänge zu approximieren, benötigen wir auch eine nicht-lineare Komponente in unserem NN.

Beliebte Aktivierungsfunktionen

• Rectified Linear Unit (\(ReLU\))
  

  \(f(x)=max(0, x)\)

• \(Leaky\ ReLU\)
  

  \(f(x)=\begin{cases} x &\quad if\ x > 0 \\ 0.1x &\quad else \end{cases}\)

• Sigmoid Function
  

  \(f(x)= \frac{1}{1+e^{-t}}\)

Function Plot

Cost Function (\(J\))

Eine Funktion um zu bestimmen wie ’nah’ wir uns an unserem erwarteten Inference Wert befinden.

In dieser Präsentation benutzen wir die Euklidean-Distance \((x-y)^2\) als Cost Function.

Forward Propagation

Ein Layer in einem Feed-Forward Neural Network besteht aus folgenden Elementen:

• Inputs (\(X\))
• Weights (\(W\))
• Biases (\(b\))
• Output (\(a\))

Berechnung des Inputs

Jedes Neuron enthält einen Vektor mit Weights \(w\), der Angibt wie stark jeder Input gewichtet wird.
\(a_1*w_1+a_2*w_2\) oder \(a_{L-1}W_L\)

Formell

Um die Aktivierungen (\(a\)) eines Layers zu berechen können wir folgende Formel benutzen:

\(a_L = \sigma(W_La_{L-1} + b_L)\)

Der berechnete Vektor \(a_L\) dient dem Layer \(L+1\) als Input.

Computational Graph

\[ a = \sigma(a_{L-1}W_L+b) \]

Beispiel (XOR)

\(W=\left[\begin{array}{ccc} 1 & 1 \\ 1 & 1 \end{array}\right]\)
\(b=\left [\begin{array}{ccc} 0 \\ -1 \end{array} \right]\)

Multiplizieren der Weights (\(W\)) und Inputs (\(X\))

\[ XW=\left[\begin{array}{ccc} 0 & 0 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{array} \right] \left[\begin{array}{ccc} 1 & 1 \\ 1 & 1 \end{array}\right]= \left[\begin{array}{ccc} 0 & 0 \\ 1 & 1 \\ 1 & 1 \\ 2 & 2 \end{array} \right] \]

Addieren des Bias Vektors (\(b\))

\[ XW + b= \left[\begin{array}{ccc} 0 & 0 \\ 1 & 1 \\ 1 & 1 \\ 2 & 2 \end{array} \right] + \left(\begin{array}{ccc} 0 \\ -1 \end{array}\right)= \left[\begin{array}{ccc} 0 & -1 \\ 1 & 0 \\ 1 & 0 \\ 2 & 1 \end{array} \right] \]

Aktivierungsfunktion (in diesem Fall \(ReLU\))

\(ReLU:= f(x)=max(0, x)\)

\[ relu(XW+b)= relu(\left[\begin{array}{ccc} 0 & -1 \\ 1 & 0 \\ 1 & 0 \\ 2 & 1 \end{array} \right])= \left[\begin{array}{ccc} 0 & 0 \\ 1 & 0 \\ 1 & 0 \\ 2 & 1 \end{array} \right] \]

Die Aktivierungsfunktion wird auf jedes Element der Matrix ausgeführt.

Output Layer

Multiplizieren der Output Matrix des ersten Layers mit den Weights des Output Layers (\(w\)). \[ w= relu(XW+b)* \left[\begin{array}{ccc} 1 \\ -2 \end{array}\right]= \left[\begin{array}{ccc} 0 & 0 \\ 1 & 0 \\ 1 & 0 \\ 2 & 1 \end{array} \right]* \left[\begin{array}{ccc} 1 \\ -2 \end{array}\right]= \left[\begin{array}{ccc} 0 \\ 1 \\ 1 \\ 0 \end{array}\right] \]

Predictions & Input

Input: \(\left[\begin{array}{ccc} 0 & 0 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{array} \right]\)
Predictions: \(\left[\begin{array}{ccc} 0 \\ 1 \\ 1 \\ 0 \end{array}\right]\)

Code Beispiel

def forward(X):
    a = X
    for layer in L:
        a = layer.weights @ a + layer.bias
    return a

Laufzeitkomplexität

\[ O(w) \]

• \(w\) Anzahl der Weights in neuronalem Netz.

Backpropagation

Wozu brauchen wir den Backpropagation Algorithmus?

Ein fundamentaler Baustein, von neuralen Netzen.

Backpropagation ist kein Lernalgorithmus/Optimierungsalgorithmus, sondern aussschlißlich für die Generierung der Gradients jedes Layers zuständig.

Also suchen wir folgende Gradients:

• \(\nabla_{b^k} J\)
• \(\nabla_{w^k} J\)

Kettenregel

Die Kettenregel ist nützlich um Ableitungen aus schon bereits vorhandenen Ableitungen zu konstruieren.

\[y=g(x)\ und\ z=f(g(x))=f(y)\]

Dann besagt die Kettenregel: \(\frac{dz}{dx} = \frac{dz}{dy} \frac{dy}{dx}\)

Kettenregel als Graph

\[ x = f(w),\ y=f(x),\ z=f(y) \]

\[ \frac{d z}{d w}= \frac{d z}{d y} \frac{d y}{d x} \frac{d x}{d w} = f'(y)f'(x)f'(w) \\ = f'(f(f(w)))f'(f(w))f'(w) \]

Anpassung der Forward Propagation

Wir benötigen folgende Werte aus jedem Layer um den Backpropagation Algorithmus ausführen zu können.

• \(a\) Aktivation Vektor
• \(z\) Pre Activation Function Vektor

\(f'(y)f'(x)f'(w)\): Speichern der Zwischenergebnisse in Variablen \(f'(f(f(w)))f'(f(w))f'(w)\): Neu Evaluierung der Zwischenergebnisse

Beschreibung des Algorithmus

Schritt 1

Forward Propagation ausführen.

Schritt 2

Wir berechnen den Gradienten der Cost Function \(J\). \(J = \frac{1}{2} (y-X)^2 \rightarrow \nabla_y J = X - y\)

Schritt 3

Erst müssen wir den Gradienten in Relation zu den pre activation function values berechnen.

\(\nabla_{a^{k}} J = g \odot f'(a^{(k)})\)

mit \(f'(x) := Ableitung\ der\ Aktivierungsfunktioin\)

Schritt 4

Weight Gradienten berechnen. \[ f(w, a, b) = w*a+b \] \(g * \frac{\partial}{\partial w} = g * (a+0)\)

\(\nabla_{w^k} J = ga^{k-1}\)

Schritt 5

Bias Gradienten berechnen. \[ f(w, a, b) = w*a+b \] \(g * \frac{\partial}{\partial b}= g * 1\)

\(\nabla_{b^{k}} J = g\)

Schritt 6

\(\nabla a^{k-1} J = w^kg\)

Wiederholen von Schritt 3 - 5 des nächsten Layers (\(L{-1}\))

Graph

Praktisches Beispiel in Python

Basic Backpropagation Implementation

Mini Batch Training

In der Praxis werden keine Vektoren als Input Daten benutzt, sondern Matrizen (siehe XOR Beispiel). \[ Input = \left[\begin{array}{ccc} 0 & 0 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{array} \right] \]

Wir erhalten nun auch mehrere Gradienten in Form einer Matrix. Wir können nun den Durchschnitt der Gradienten nutzen um unsere Weights anzupassen.

Iris Dataset

Mini Batch Backpropagation Implementation

Low Learning Rate

High Learning Rate

Komplexität

Wichtig
Folgende Komplexitäten beziehen sich ausschließlich auf den Backpropagation Algorithmus.

Laufzeitkomplexität

Backpropagation besitzt die gleiche Laufzeitkomplexität wie Forward-propagation.

\[ O(w) \]

• \(w\) Anzahl der Weights in neuronalem Netz.

Speicherkomplexität

\[ O(mh) \]

• \(m\) Anzahl an Elementen in Batch
• \(h\) Anzahl der Hidden-Units

General Backpropagation

Bisher haben wir uns nur mit Backpropagation in Zusammenhang mit neuronalen Netzwerken beschäftigt.
Backpropagation kann aber auch generell für andere Anwendungen eingesetzt werden.

Symbol to Number / Symbol to Symbol

Es existieren zwei verschiedene Möglichkeiten die Berechnungen der Gradients durchzuführen.

• Symbol to Number
• Symbol to Symbol

Symbol to Number

Die Input Variablen werden durch Zahlenwerte ersetzt und daraufhin (wie besprochen) alle nötigen Gradienten berechnet.

Symbol to Symbol

Beim der Symbol to Symbol Herangehensweise wird zuerst der Graph mit allen Ableitungen mit der Hilfe von symbolischen Werten konstruiert.
Später wird dann der Graph mit der Hilfe eines eigenen Algorithmus ausgewertet.

Vorteil
Ableitungen eines höheren Grads können berechnet werden, indem man den Backpropagation Algorithmus auf einen bereits abgeleiteten Graphen ausführt.

Operationen

Wir betrachten einen computational Graph, jede Node in dem Graph repräsentiert eine Variable in Form eines Tensors.

Funktionen

• get_operation()
• get_consumers()
  Gibt alle Variablen/Operationen zurück, die ’Kinder’ von sich selber sind.
• get_inputs()
  Gibt alle Variablen/Operationen zurück, die ’Eltern’ von sich selber sind.
• bprop()
  Muss bei jeder Operation implementiert werden.

Algorithmus

Benötigt ist:

• die Menge aller Variablen \(T\), deren Gradienten wir berechnen müssen
• den Graphen \(G\)
• die Variable \(z\), die wir differenzieren wollen

Äußere Funktion

Wir definieren \(G'\) als alle Variablen, die Vorfahren von \(z\) und Nachfahren von \(T\) sind.

In grad_table können wir Variablen Gradients zuweisen.

grad_table[z] = 1 (da \(\frac{\partial z}{\partial z} = 1\))

Loop über alle Variablen, deren Gradienten wir berechnen müssen

In jedem Loop rufen wir die Funktion build_grad auf.

for v in T:
    build_grad(v, G, G_1, grad_table)
return [grad_table[v] for v in T]

build_grad(v, G, G_1, grad_table)

def build_grad(v, G, G_1, grad_table):
    if v in grad_table: return grad_table[v]
    i = 1
    for c in get_consumers(v, G_1):
        op = get_operation(c)
        d = build_grad(c, G, G_1, grad_table)
        g[i] = op.bprop(get_inputs(c, G_1), v, d)
        i += 1
    g = sum(g)
    grad_table[v] = g
    return g

bprop Funktion

op.bprop(inputs, X, G)

inputs: Liste an Inputs, die wir der Operation zur Verfügung stellen
X: Input, dessen Ableitung wir berechnen wollen
G: Gradient des Outputs der Operation

Beispiel

Graph

Wir wollen \(\frac{\partial u_1}{\partial u_4}\) bestimmen.

Bestimmen der Ableitung \(\frac{\partial u_1}{\partial u_4}\)

Eintragen aller Ableitungen in Graph

Generalisierbarkeit

Dadurch ist der Backpropagation Algorithmus sehr allgemein anwendbar.

Jede Operation ist für seine eigene Differenzierung verantwortlich und benötigt keine weiteren Informationen.

Historisches

• Kettenregel stammt aus dem 17ten Jahrhundert (Leibniz, 1676).
  
• Lineare neurale Netzwerke Mitte des 20ten Jahrhunderts.
  
• Erfolgreiche Experimente mit Back-Propagation (1986)
  

Popularität von neuronalen Netzen

Klassische machine learning Algorithmen wurden in den 90er Jahren mehr genutzt als neuronale Netzwerke.

Durch die hohe Speicheranforderung wurden NN ab ca. 2006 immer vermehrter eingesetzt und bilden heute einen fundamentalen Baustein von maschinellem Lernen.

Backpropagation & Gradient Descent

Beide treibenden Algorithmen von neuronalen Netzwerken haben sich seit den 80er Jahren nicht wesentlich verändert.

Bessere Resultate sind besser Hardware und Dataset Optimierung zu verdanken.

Quellen

• Deep Learning (Ian Goodfellow, Yoshua Bengio & Aaron Courville)
• Back-Propagation is very simple. Who made it Complicated? (Prakash Jay)
• Wikipedia: https://en.wikipedia.org/wiki/Backpropagation
• Wikipedia: https://en.wikipedia.org/wiki/Delta_rule